chuap
chuap — Simulates Chua's oscillator, an LRC oscillator with an active resistor, proved capable of bifurcation and chaotic attractors, with k-rate control of circuit elements.
Description
Simulates Chua's oscillator, an LRC oscillator with an active resistor, proved capable of bifurcation and chaotic attractors, with k-rate control of circuit elements.
Initialization
iI3 -- Initial current at G
iV2 -- Initial voltage at C2
iV1 -- Initial voltage at C1
Performance
kL -- Inductor L
kR0 -- Resistor R0
kC1 -- Capacitor C1
kG -- Resistor G
kGa -- Resistor V (nonlinearity term)
kGb -- Resistor V (nonlinearity term)
kGb -- Resistor V (nonlinearity term)
ktime_step -- Delta time in the difference equation, can be used to more or less control pitch.
Chua's oscillator is a simple LRC oscillator with an active resistor. The oscillator can be driven into period bifurcation, and thus to chaos, because of the nonlinear response of the active resistor.
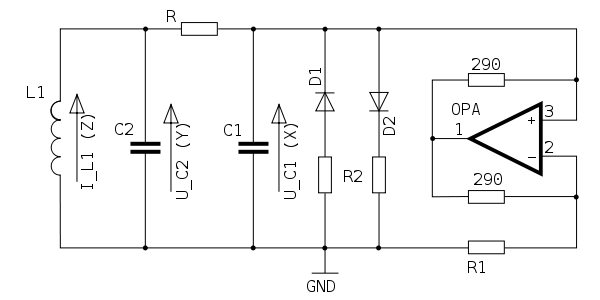
Diagram of Chua's Oscillator Circuit
The circuit is described by a set of three ordinary differential equations called Chua's equations:
dI3 R0 1
--- = - -- I3 - - V2
dt L L
dV2 1 G
--- = -- I3 - -- (V2 - V1)
dt C2 C2
dV1 G 1
--- = -- (V2 - V1) - -- f(V1)
dt C1 C1
where f() is a piecewise discontinuity simulating the active resistor:
f(V1) = Gb V1 + - (Ga - Gb)(|V1 + E| - |V1 - E|)
A solution of these equations (I3,V2,V1)(t) starting from an initial state (I3,V2,V1)(0) is called a trajectory of Chua's oscillator. The Csound implementation is a difference equation simulation of Chua's oscillator with Runge-Kutta integration.
![[Note]](images/note.png)
|
Note |
|---|---|
|
This algorithm uses internal non linear feedback loops which causes audio result to depend on the orchestra sampling rate. For example, if you develop a project with sr=48000Hz and if you want to produce an audio CD from it, you should record a file with sr=48000Hz and then downsample the file to 44100Hz using the srconv utility. |
![[Warning]](images/warning.png)
|
Warning |
|---|---|
| Be careful! Some sets of parameters will produce amplitude spikes or positive feedback that could damage your speakers. |
Examples
Here is an example of the chuap opcode. It uses the file chuap.csd.
Example 116. Example of the chuap opcode.
<CsoundSynthesizer> <CsOptions> ; Select audio/midi flags here according to platform -odac ;;;RT audio out ;-iadc ;;;uncomment -iadc if RT audio input is needed too ; For Non-realtime ouput leave only the line below: ; -o chuas_oscillator.wav.wav -W ;;; for file output any platform </CsOptions> <CsInstruments> sr = 44100 ksmps = 32 nchnls = 2 0dbfs = 1 gibuzztable ftgen 1, 0, 16384, 10, 1 instr 1 ; sys_variables = system_vars(5:12); % L,R0,C2,G,Ga,Gb,E,C1 or p8:p15 ; integ_variables = [system_vars(14:16),system_vars(1:2)]; % x0,y0,z0,dataset_size,step_size or p17:p19, p4:p5 istep_size = p5 iL = p8 iR0 = p9 iC2 = p10 iG = p11 iGa = p12 iGb = p13 iE = p14 iC1 = p15 iI3 = p17 iV2 = p18 iV1 = p19 iattack = 0.02 isustain = p3 irelease = 0.02 p3 = iattack + isustain + irelease iscale = 1.0 adamping linseg 0.0, iattack, iscale, isustain, iscale, irelease, 0.0 aguide buzz 0.5, 440, sr/440, gibuzztable aI3, aV2, aV1 chuap iL, iR0, iC2, iG, iGa, iGb, iE, iC1, iI3, iV2, iV1, istep_size asignal balance aV2, aguide outs adamping * asignal, adamping * asignal endin </CsInstruments> <CsScore> ; Adapted from ABC++ MATLAB example data. i 1 0 20 1500 .1 -1 -1 -0.00707925 0.00001647 100 1 -.99955324 -1.00028375 1 -.00222159 204.8 -2.36201596260071 3.08917625807226e-03 3.87075614929199 7 .4 .004 1 86 30; torus attractor ( gallery of attractors ) i 1 + 20 1500 .425 0 -1 1.3506168 0 -4.50746268737 -1 2.4924 .93 1 1 0 -22.28662665 .009506608 -22.2861576 32 10 2 20 86 30 ; heteroclinic orbit i 1 + 20 1024 .05 -1 -1 0.00667 0.000651 10 -1 .856 1.1 1 .06 51.2 -20.200590133667 .172539323568344 -4.07686233520508 2.5 10 .2 1 66 81 ; periodic attractor (torus breakdown route) i 1 + 20 1024 0.05 -1 -1 0.00667 0.000651 10 -1 0.856 1.1 1 0.1 153.6 21.12496758 0.03001749 0.515828669 2.5 10 0.2 1 66 81 ; torus attractor (torus breakdown route)' </CsScore> </CsoundSynthesizer>
Credits
| Inventor of Chua's oscillator: Leon O. Chua |
| Author of MATLAB simulation: James Patrick McEvoy MATLAB Adventures in Bifurcations and Chaos (ABC++) |
| Author of Csound port: Michael Gogins |
New in Csound version 5.09
Note added by François Pinot, August 2009