Introduction
Pseudo-stereophony audio processing techniques generate two stereochannels from a single mono one, in order to generate a wider spatialimpression. The need for pseudo-stereo techniques arose with thedevelopment of commercial stereo reproduction and distribution, toattempt to bring existing mono audio material into the new medium.Nonetheless, pseudo-stereo can also be used as a creative audiomanipulation tool in itself. It is important to note thatpseudo-stereo techniques are also sometimes called pseudo-stereosynthesizers precisely because they artificially create the spatialinformation. Even though stereo width manipulation using Mid-Sidebalancing (starting with a Mid (L+R) signal and adding/subtractingvarying amounts of Side (L-R) signal to increase width) is sometimesreferred to in literature as pseudo-stereo, it is not a pseudo-stereotechnique, because it uses spatial characteristics–in the form ofphase difference–already present in the original stereo signals.
Pseudo-stereo has been explored in two different scenarios:loudspeaker and headphone reproduction. The type of reproduction willsignificantly affect the result of the process, because usingloudspeakers, both ears are getting the signal from both speakers,producing comb filtering, while headphone reproduction has isolationbetween the signals, but does not provide HRTF cues and is free fromroom reverberation. So the perceived effect of pseudostereotechniques will be different for loudspeaker and headphone listening.Pseudo-stereophony techniques tend to have a bad reputation in audioengineering circles because although they significantly enhancespatial perception, they produce unacceptable side effects likephasiness, a sound that is tiring to listen to or unacceptabledegradation of the sound.
Pseudo-stereo in practice
The exact approach and effect of pseudo-stereo techniques hasalways been somewhat vague. While some authors have developedpseudo-stereo techniques in an attempt to increase the perceivedwidth of the audio source, others have attempted to achieve differentspatial locations for different spectromorphologically relatedelements of the audio source. So, even though some authors seekeither image spread or image separation, in practice, you will tendto have both with complex audio material, with hard to predict andinconsistent results. For this reason, usage of pseudo-stereoalgorithms requires careful attention to detail and fine tuning toachieve results that will not be regretted down the road.
It is understood that differences between the sound at each earare interpreted as spatial information. These differences are usuallycharacterized using the Inter-Aural Cross-correlation Coefficient(IACC), which is the maximum absolute peak of the cross-correlationbetween both signals. Pseudo-stereo techniques produce perception ofspace precisely because they generate slight differences between thesignals at each ear which the brain interprets as spatial cues.
I. Time Delay between speakers
The simplest pseudo-stereo technique consists of adding a smalldelay to a signal. Lauridsen experimented with this technique [1],reproducing it not over a conventional stereo system, but on a pairof speakers radiating at a 90° angle, using delays between 50ms and150ms as shown in Figure 1. The farther speaker, which points to theside, was used unbaffled, so it can project a wavefront &ndash inverted inphase with relation to its front&ndash on its rear.

If the playback occurs in free-field conditions, e.g. an anechoicchamber, and the speakers have ideal directivity characteristics, oneear of the listener would receive the far speaker in phase, while theother side would receive it in anti-phase. This signal from the farspeaker would add to the signal from the delayed near speaker, toproduce comb filtering. Thus, since both channels effectively havedifferent frequency responses, each channel's signals aredifferent, and this will produce IACC differences. This effect is infact enhanced since the room provides further decorrelation throughreverb and irregularities in speaker directivity.
Though this technique may be useful to counter the precedenceeffect, its results are location dependent, as a delay that workswell for a certain location will not work for another. It is alsosource-material dependent as some delay times will colour certainmaterial in unacceptable ways, while being suitable for others.
II. Complementary filters
Complementary Comb Filters
The natural extension to the previous technique was also proposedby Lauridsen. Instead of having the signals from both loudspeakersadded in the air when reaching the ear, he proposed adding themelectronically for headphone reproduction, as shown in Figure 2.Adding a signal to a delayed version of itself is in effect a combfilter. By adding the signals electornically, what happens is that a pair of complementary combfilters is realized. This means that a dip in one channel matches apeak in the other. The system can have control of the size andnumber of filter bands by adjusting the delay time.
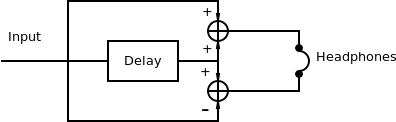
Below is an implementation of the Lauridsen technique ofcomplementary comb filters:
opcode lauridsen, aa, ak ain, kdelay xin imaxdel = 30 kdelay limit kdelay, 0.001, imaxdel adelay1 vdelay3 ain, kdelay, imaxdel aleft = -ain + adelay1 aright = ain + adelay1 xout aleft*0.5, aright*0.5endop
Schroeder studied the factors that play a greatest role in spatialimpression in these types of complementary filters for headphonereproduction [2]. He showed that it was the intensity variations infrequency rather than the phase differences between each channel thathad the greatest effect. Taking advantage of this he designed a setof complementary comb filters, as shown in Figure 3, which producethe same phase response on both channels. This system can havecontrol of the size and number of filter bands by adjusting thedelay time.
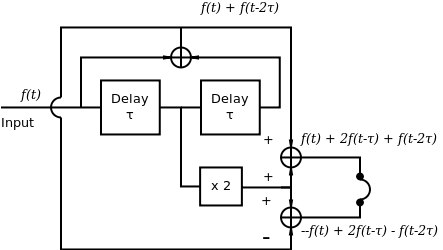
Below is shown an implementation of the Schroeder complemenary comb filters as a Csound UDO:
opcode schroeder, aa, ak ain, kdelay xin imaxdel = 30 kdelay limit kdelay, 0.001, imaxdel adelay1 vdelay3 ain, kdelay, imaxdel adelay2 vdelay3 adelay1, kdelay, imaxdel aleft = -ain + (2 * adelay1) - adelay2 aright = ain + (2 * adelay1) + adelay2 xout aleft*0.5, aright*0.5endop
There are two significant issues with these techniques, which arealso the reason why these techniques are not favoured by criticallisteners. They both produce strong coloration: the signal soundsnoticeably different from the original, and phasiness is present due to thesharp comb filters. Consequently, they are rarely used nowadays.Although their effect is quite dramatic and noticeable it is alsotiring to listen to after a while.
All-pass networks
Bauer proposed the usage of all-pass networks to produce phasedifference between two channels [3]. He proposed this technique forloudspeaker reproduction, so his reports that spatial impression wasnotably affected does not seem to contradict Schroeder's findingsfor headphones, as there will be filtering in the amplitude throughthe addition in the air of both signals. He does note however thatmore reverberant rooms tend to lessen the effect.
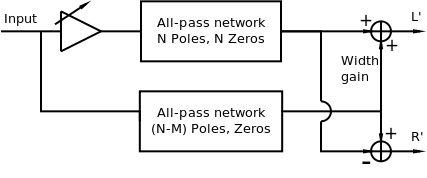
Orban proposed an enhancement to this technique that adds theall-pass networks, and through a gain control allows controlling theamount of image spread [4]. His method is shown in Figure 4. Orbansuggests setting N = 4 and M= 2,3,4.
An all-pass filter can be produced in Csound using the followingUDO:
opcode AllPass, a, a ain xin ; Generate stable poles irad exprand 0.1 irad = 0.99 - irad irad limit irad, 0, 0.99 ;iang random -$M_PI, $M_PI iang random -$M_PI, $M_PI ireal = irad * cos(iang) iimag = irad * sin(iang) print irad, iang, ireal, iimag ; Generate coefficients from poles ia2 = (ireal * ireal) + (iimag * iimag) ia1 = -2*ireal ia0 = 1 ib0 = ia2 ib1 = ia1 ib2 = ia0 printf_i "ia0 = %.8f ia1 = %.8f ia2= %.8f\n", 1, ia0, ia1, ia2 aout biquad ain, ib0, ib1, ib2, ia0, ia1, ia2 xout aoutendop
This UDO produces the filter coefficients for an IIR biquad filter byrandomly generating stable poles which guarantee an all-passresponse. This UDO in particular produces a 2-pole all-pass filter.
This UDO can then be used to realize the Orban method like below(including selection of number of poles for the second filter):
opcode Orban, aa, akk ain, kwidth, kmode xin ;; Cascade two filters to create a 4-pole all-pass a1 AllPass ain a1 AllPass a1 a2 AllPass ain if kmode == 1 then a2 AllPass a2 endif aout1 = a1*kwidth + a2 aout2 = - a1*kwidth + a2 xout aout1, aout2endop
It is important to note that since the filter coefficients arerandom, there are infinitely many different filters which could beused in combination. Usually, the best combination must be determinedby trial and error as different filters will have different effects ondifferent material.
Gerzon proposed a further refinement which allows very precisecontrol over the characteristics of the complementary filters [5]. Ituses two identical all-pass filters, as the basis for construction ofcomb filters. It is shown in Figure 5. Like the Orban method, thespread can be controlled using gain on one of the paths to eachchannel. It must be noted that this method is no longer completelymono-compatible, although it can have less artifacts than theprevious one.
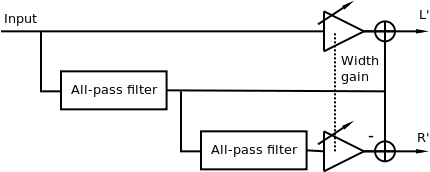
The method can be realized in Csound using a UDO below, which hasa mode parameter to select the number of poles of the all-passfilters by chaining two-pole all-pass filters:
opcode Gerzon, aa, akk ain, kwidth,kmode xin a1 AllPass ain a2 AllPass a1 if kmode > 0 then a1 AllPass a1 a2 AllPass a1 endif if kmode > 1 then a1 AllPass a1 a2 AllPass a1 endif if kmode > 2 then a1 AllPass a1 a2 AllPass a1 endif if kmode > 3 then a1 AllPass a1 a2 AllPass a1 endif if kmode > 4 then a1 AllPass a1 a2 AllPass a1 endif if kmode > 5 then a1 AllPass a1 a2 AllPass a1 endif if kmode > 6 then a1 AllPass a1 a2 AllPass a1 endif aout1 = ain*kwidth + a1 aout2 = -a2*kwidth + a1 xout aout1, aout2endop
Gerzon mentions that one of the purposes of this technique is to do"simulation of the size of a sound source" [5]. Both SchroederandGerzon envisioned this process as one that could also be appliedindividually to individual mono components of a stereo mix.
In essence as Gauthier states [6], any combination of invertedfiltering can serve as pseudo-stereo filters for artistic purposes.This could be done both with time domain filtering or with frequencydomain filtering.
III. Frequency modulation
Artificial Double Tracking (ADT) is a recording techniquedeveloped to generate a second channel of lead vocal from one take,using a second synchronized tape machine. The second machine wouldhave small delay and a amount of wow and flutter effectivelymodulating the signal. The original signal is sent to one channel,while the second signal goes to the other. The variations infrequency between both signals will create a modulated comb filter,which in turn produces variations in IACC, perceived as spatialproperties if the modulation is small enough. The wow and flutter canbe modeled as simple periodical modulation, or using some form ofinterpolated jitter:
opcode modulate, a, akkkki ain, kfreq, kamp, ktype, kdelay, imaxtime xin if ktype == 0 then amod jspline kamp, kfreq, kfreq elseif ktype == 1 then amod poscil kamp, kfreq, 1 elseif ktype == 2 then amod poscil kamp, kfreq, 2 endif aout vdelay3 ain, kdelay *(1.00001 + amod), imaxtime xout aoutendop
The processing would then look like:
aflutter modulate gainput, gkflutter_freq, gkflutter_amt, gkflutter_type, gkdelay_adt, 100 awow modulate aflutter, gkwow_freq, gkwow_amt, gkwow_type, gkdelay_adt, 100 aout1 = gainput*gklevel_adt aout2 = awow*gklevel_adt
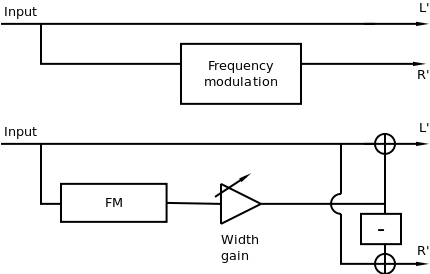
A variation of this technique, implemented byhbasm's Stereoizer plugin,adds phase inverted chorus to the dry signal on each channel. Monodownmix will result in the original signal, while chorusing will beheard on each individual channel. These techniques are pictured inFigure 6.
aflutter modulate gainput, gkflutter_freq, gkflutter_amt, gkflutter_type, gkdelay_adt, 100 aout1 = (gainput + (aflutter*gkwidth_adt) )*gklevel_adt aout2 = (gainput - (aflutter*gkwidth_adt) )*gklevel_adt
IV. Artificial decorrelation
Artificial decorrelation is defined by Kendall as the "processwhereby an audio source signal is transformed into multiple outputsignals with waveforms that appear different to each other but whichsound the same as the source" [7]. In the same article, Kendallproposes a method to spread a monophonic source over multipleloudspeakers using artificial decorrelation. Kendall proposed usingFIR filters derived from doing inverse FFT from a spectrum which isflat, but with phases randomized between +Π and -Π.Additionally, the amount of decorrelation can be controlled by mixingthe phase vectors before doing the IFFT to decrease thedecorrelation. Alternatively, instead of designing a filter thisway, a set of coefficients which can provide decorrelation can beobtained from MLS (Maximal length sequences) or Golay codessequences.
In this technique there is a trade-off between transientpreservation and representation of low frequency. To produce asufficiently adequate frequency response these filters must have atleast 1024 points, which might cause smearing of transients for somematerial. Another issue with this method is that it will have sideeffects, as Kendall notes, because although the points for thecalculated filter will lie at an amplitude of 1, points in between(when the filter is upsampled, or when doing DAC), are not, so thefilters are not in effect flat. Additionally, since the phases aredifferent, they will produce different cancellations andreinforcements varying with frequency. For this reason, Kendallstates that a "good-sounding'' pair of filter coefficients must bechosen through subjective evaluation. The author does mention thatthis timbral coloration is less noticeable if the filtering isapplied to individual tracks instead of processing the entire mix.
Kendall also proposed constructing dynamic filters from IIRall-pass filters, interpolating between random coefficients to have aconstantly varying phase response to produce a similar effect.
Although these techniques are a natural evolution of previoustechniques using all-pass filters, particularly to those proposed byBauer, since they attempt to leave the amplitude spectrum unchanged,they are the first to include the concept of decorrelation as animportant attribute in the perception of ASW. It is also significantthat these techniques, since they do not involve complementaryfilters, can be used on a greater number of channels, and thereforecan go beyond Pseudo-stereo.
To implement artificial decorrelation filters in Csound, it isnecessary to use python, since pure Inverse FFTs (without phasevocoder) are required, which is a low level operation not available inCsound. To use the implementation presented, it will be necessary tohave the python opcodes installed in addition to the numpy pythonlibrary for FFT and IFFT computation.
The filter coefficients and python functions for data exchangewith Csound are presented below:
#! /usr/bin/env python import sys from numpy import *from numpy.fft import ifftimport numpy.random as random ## global configuration and variables max_chnls = 16Xn = []yn = [] for i in range(max_chnls): Xn.append(array([])) yn.append(array([])) ## Csound functionsdef new_seed(seed_in = -1):# print "New seed: ", int(seed_in) if seed_in == -1: random.seed() #can put seed here, leaving blank uses system time else: random.seed(longlong(seed_in)) #can put seed here, leaving blank uses system time return float(seed_in); def get_ir_length(channel = -1): index = int(channel) if channel != -1 else 1 return float(len(Xn[index])) def get_ir_point(channel, index): global yn return float(yn[int(channel - 1)][int(index)].real) def new_ir_for_channel(N, channel = 1, max_jump=-1): global Xn, yn [Xfinal, y] = new_ir(N, max_jump) Xn[int(channel) - 1] = Xfinal yn[int(channel) - 1] = y def new_ir(N, max_jump=-1):# ''' new_ir(N)# N - is the number of points for the IR,# max_jump - is the maximum phase difference (in radians) between bins# if -1, the random numbers are used directly (no jumping).# ''' if N < 16: print "Warning: N is too small." print "Generate new IR size=", N n = N//2 # before mirroring Am = ones((n)) Ph = array([]) limit = pi Ph = append(Ph, 0) old_phase = 0 for i in range(1,n): if max_jump == -1: Ph = append(Ph, (random.random()* limit) - (limit/2.0)) else: # make phase only move +- limit delta = (random.random() * max_jump * 2* pi) - (max_jump * pi) new_phase = old_phase + delta Ph = append(Ph, new_phase) old_phase = new_phase #pad DC to 0 and double last bin Am[0] = 0 Xreal = multiply(Am, cos(Ph)) Ximag = multiply(Am, sin(Ph)) X = Xreal + (1j*Ximag) Xsym = conj(X[1:n])[::-1] # reverse the conjugate X = append(X, X[0]) Xfinal = append(X,Xsym) y = ifft(Xfinal) return [Xfinal, y.real]
The decorrelation algorithm in Csound using the above pythonscript will be:
sr = 44100ksmps = 2560dbfs = 1nchnls = 2 #define MAX_SIZE #4096# gisize init 1024gkchange init 0 pyinitpyexeci "decorrelation.py" giir1 ftgen 100, 0, $MAX_SIZE, 2, 0giir2 ftgen 101, 0, $MAX_SIZE, 2, 0 gifftsizes ftgen 0, 0, 8, -2, 128, 256, 512, 1024, 2048, 4096, 0 opcode getIr, 0, iiichan, ifn xinindex init 0idummy init 0isize pycall1i "get_ir_length", -1isize = gisizedoit: ival pycall1i "get_ir_point", ichan, index tableiw ival, index, ifn loop_lt index, 1, isize, doit endop instr 1 ; Inputs and control gainput inch 1; gainput diskin2 "file.wav", 1 gkon_decorrelation invalue "on_decorrelation" gklevel_decorrelation invalue "level_decorrelation"endin instr 2 ; Generate new IR and load it to ftable giirinew_seed = p4 kfftsize invalue "fftsize"gisize table i(kfftsize), gifftsizes ; Clear tablesgiir1 ftgen 100, 0, $MAX_SIZE, 2, 0giir2 ftgen 101, 0, $MAX_SIZE, 2, 0 kmax_jump1 init -1kmax_jump2 init -1 icur_seed pycall1i "new_seed", inew_seed ;-1 means use system time ;Chan 1imax_jump = i(kmax_jump1)ichan = 1pycalli "new_ir_for_channel", gisize, ichan, imax_jumpgetIr 1, giir1 ;Chan 2imax_jump = i(kmax_jump2)ichan = 2pycalli "new_ir_for_channel", gisize, ichan, imax_jumpgetIr 2, giir2 gkchange init 1turnoff endin instr 17 ; Kendall method if gkchange == 1 then reinit dconvreinit gkchange = 0endif dconvreinit:prints "Reinit ftconv\n" if gkon_decorrelation == 1 then aout1 ftconv gainput, giir1, 1024, 0, gisize aout2 ftconv gainput, giir2, 1024, 0, gisize aout1 = aout1*gklevel_decorrelation aout2 = aout2*gklevel_decorrelationelse aout1 = gainput*gklevel_decorrelation aout2 = gainput*gklevel_decorrelationendifoutch 1, aout1, 2, aout2endin
Other types of decorrelation
Other similar techniques have been proposed, like decorrelationusing Feedback delay networks, sub-band decorrelation, randomshifting of critical bands and artificial decorrelation in thefrequency domain.
Examples
Examples from this article can be downloaded here.
References
[1] H. Lauridsen, "Nogle forsog reed forskellige former rumakustik gengivelse," Ingenioren, vol. 47, p. 906, 1954.
[2] M. R. Schroeder, "An artificial stereophonic effect obtainedfrom using a single signal," in AES Convention 9, 1957.
[3] B. B. Bauer, "Some techniques toward better stereophonicperspective." IEEE Transactions on Audio, vol. 11, pp. 88–92, May1963.
[4] R. Orban, "A rational technique for synthesizingpseudo-stereo from monophonic sources," Journal of the Audio EngineeringSociety , vol.18, pp. 157–164, April 1970.
[5] M. A. Gerzon, "Signal processing for simulating realisticstereo images," in AES Convention 93, 1992.
[6] P.-A. Gauthier, "A review and an extension of pseudo-stereofor multichannel electroacoustic compositions: Simple DIY ideas,"eContact!, vol. 8.3, 2005.
[7] G. Kendall, "The decorrelation of audio signals an itsimpact on spatial imagery," Computer Music Journal, vol. 19:4, pp. 71–87,1995.