Introduction
This article is about employing Csound to create test tones for audio tests and measurement purposes. Csound excels in the creation of digital audio signals due to the many opcodes available for the creation and manipulation of sound as a software synthesis application. Thus Csound works well for specialized test tone creation. Several test tones are described below such as sweeps, chirps, noise, multitones, and one-third octave divisions. Examples are provided for several test tones as well as references for a more in-depth explanation of the particular topics briefly covered in the article.
I. Oscillators
The basic tool for test tone generation is the sine wave oscillator. Sine waves are useful as test tones because of their pure, simple, fundamental harmonic makeup, and their ability to be seen clearly upon graphs in the time and frequency domains. Csound has many different types of oscillators, the most common being table lookup oscillators. For a brief overview of the different types of oscillators see "Tour of Oscillators" , Csound Journal, Issue 3, Spring 2006[1].
II. Test Tone Building
Sweeps and Chirps
Csound does exceptionally well with test tone generation due to the numerous high quality software synthesis opcodes which help make specialized test tone sound creation an easy task. Sweeps and chirps are part of the same, general, swept sine method of test tone generation. Basically an envelope-- linear or exponential, is employed as a multiplier of the frequency input parameter for an oscillator in order to change the frequency of the signal over time. Sweeps are generally of longer duration for measuring frequency response of devices while chirps are of very short durations and employed effectively to characterize systems (filters), among other uses.In the code excerpt below, the frequency sweep will range from 20 Hz to 20 KHz and back again, over 10 seconds; and if 0dbfs = 215 (32768), then the output volume can be verified as around -1.0 dbfs less than full scale using the dbfsamp opcode (dbfsamp(32768-3565)).
kpitch linseg 0.001, p3*.34, 1.0, p3*.33, 1.0, p3*.33, 0.001aout oscili 0dbfs - 3565, 20000 * kpitch, 1...f 1 0 8192 10 1i1 0 10
Csound allows for the building of sweep segments which can be divided into portions which dwell on particular frequencies before continuing the sweep. This can be accomplished using a number of different approaches including the use of exponential and linear generators. This type of signal is useful for troubleshooting crossover frequencies or identifying perceived particular problematic frequencies for sound systems. For example if a known passive crossover frequency between low-mid, and high frequency speakers in a cabinet is 1.2 KHz, then creating a sweep which pauses just below 1.2 KHz, then just above; the crossover can be verified as working effectively. This type signal, a sweep and a pause, is able to do two types of testing at once: to check all frequencies quickly, and to check the function of specific frequencies. Thus Csound is a good tool for building complex signals which can perform multiple tasks.
See the list of example .csd files at the end of this article, and download all example files here: workbench_exs.zip
Noise
Noise, especially pink noise, is useful for testing sound systems because of the equal energy per octave characteristic of pink versus white noise which has equal energy per hertz. White noise, used to calibrate equipment, generally exhibits a 3 db per octave buildup, while pink noise exhibits a 3 db per octave rolloff[2]. Pink noise is often used to ringout monitors to control feedback and also to "tune" a room or adjust graphic EQ settings to help achieve a relatively flat frequency response in a sound systems, given the particular resonant characteristics of a room. Csound employs several methods to generate noise including the noise (white) and pinkish(pink) opcodes. Since noise is comprised of random signals, at various levels and phases, Csound's random generators, such as the x-class noise generators, can also be employed to generate shaped noises from particular random distributions.Pulse Train and Sinc Function
The buzz opcode can create a set of harmonically related sine partials for producing rich sounds, and if the total number of input harmonics requested is equal to the Nyquist (sr/2), and the input frequency is low (ex. 1 cps), then a pulse train is discernable from the output of the rich tones generated by buzz. A single pulse created in this manner is suitable and useful as a click for testing phase, for example, between biamped horn and woofer speakers, or as an impulse for creating convolution reverbs.
The sinc function is available as a Gen20 window function, or can be reproduced manually in Csound with some effort for constructing a waveform, such as a sine wave, employing the sinc as a sampling function.
sin(pi*x)/(pi*x)
The full source code and explanation of linear, cubic, and sinc interpolation manually is viewable in Han's Mikelson's article "Interpolation" from Csound Magazine, Summer 2000, in which there is a demonstration of sine wave construction by summing sinc signals[3].
Multitones
Another form of tone useful for testing is the multitone signal which consists of a number of known frequencies at a particular frequency spacing which allows for distortion observation and measurement in the frequency domain for a given device under test. There are a few different methods for constructing multitone signals such as utilizing Csound's score features to list the frequencies to be performed simultaneously by one instrument, creating a complex tone as an f-statement using a Gen routine and performing it with an oscillator, or employing multiple instruments--each as an oscillator, which all play at the same time. The later method of utilizing separate instruments, each as an oscillator, is similar to analog processes for multitone creation, and proves to be the most accurate within Csound for maintaining a level signal in the frequency domain.
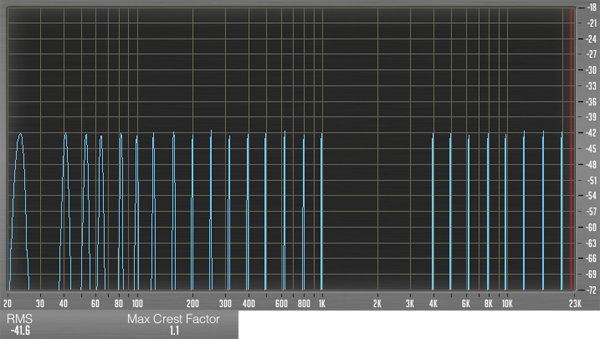
One issue with multitone signals for test purposes is the crest factor. The crest factor is the peak amplitude/RMS value of the waveform. What is desirable with multitone testing is a flat spectral peak of equal magnitude value for all tones in the mult signal in order to discern, for example, amplifier power efficiency across particular frequencies[4]. In other words low crest factors are desired for multitones.
Nth root tones
Csound works very well for varying the frequency component in the creation of test tones. Since pitch is a logarithmic scale, for twelve equal divisions of the octave the 12th root of 2, as a base 2 method, is used to calculate adjacent frequencies in the scale. For other numbered equal divisions, use that number as the nth root (ex. for 19 tone equal temperament use kctr/19.0).kpitch = kfreq * (exp(log(2.0) * (kctr)/12.0))
Another outstanding feature of Csound on the workbench is the ability to indicate any frequency desired for testing. Using a basic oscillator's xcps input parameter, it is possible to list various frequencies 220.0, 221.0, 220.01, etc. directly as input cycles per second for xcps. Csound therefore provides a rich middle ground as a test application, where in lower level programs an algorithm has to be created to generate an array of numbers, or alternatively in higher level graphical user interface applications you may not have access to finer gradations of frequency, but may only be able to select from a list of possible drop down frequencies in a menu.
Because of the ability to create and enter fine gradations of frequency, another nth root class of test tones is available which are the 1/3, and 1/n octave tones similar to frequencies found on a graphic EQ. For one-third octave frequencies the cube root is used as the nth root as a base2 method.
kband = kfreq * (exp(log(2.0) * (kctr)/3.0))Other common divisions of equalizers include one-sixth, and one-twenty fourth octave divisions. The mathematical divisions generally differ from the preferred EQ frequencies common on hardware, due to rounding and shifting of particular frequencies. Also possible is a base 10 method for arriving at nth root, one-third octave frequencies[5].
kband = kfreq * 10 ^ (3.0/(10*3.0))For room tuning by arriving at a flat frequency response to pink noise, it is interesting to explore the possibilities of the actual mathematical frequencies versus the preferred hardware graphic EQ ones.
Panning
Csound is rich with output control as well as panning opcodes. For location modulation, testing of individual speakers, as well as testing delays; the ability to position a test tone at a particular speaker placement is valuable for testing purposes. For surround speaker location testing, Csound includes the outc opcode, among others, which writes audio data with an arbitrary number of channels to an external device or stream, as well as the "format" command-line flag to save audio file output to one of the formats available in libsndfile.Classic Waves
In addition to noise, complex audio signals composed of sinusoids are useful for creating test tones for various purposes. Csound employs table lookup methods, among several other methods, as a waveform synthesis method, whereby a complex wave may be generated employing an oscillator or phasor at a given frequency to repeat a single period of a complex waveshape defined in the table[6]. While Csound does a good job of varying sample rates, frequency, amplitude, phase, and providing bandlimiting for complex waves; dedicated hardware signal generators, such as an RC (resistor-capacitor) oscillator circuit or a triangle function generator with filters may be required for very high levels of precision, since the tones generated by Csound in DSP are only as good as the analog converters which may be used to perform the signal.Conclusion
Csound excels in digital audio creation and can therefore be utilized effectively to generate high quality test tones. This article provides explanations and examples of several common test tones. Csound has many other opcodes such as dcblock, gain, hilbert, butterlp, and butterhp etc. which are suitable and useful for test and measurement applications. Other types of test signals such as quick attack, slow release, transients and hold, frequency steps etc. are also possible within Csound. Thus Csound functions as a very good, and versatile middle ground application for test signal building compared to other lower level and higher level applications. Somewhat lacking in Csound, at present, is an easy means to analyze, display, zoom, and print graphs of test signals and audio analysis since the existing functions (display, and dispfft opcodes) have not been upgraded in some time. However several good freeware applications are available and can be used to supplement Csound for that purpose.References
[1] Hearon, Jim. "Tour of Oscillators", Csound Journal, Issue 3, Spring 2006
[2] Davis, Gary & Jones, Ralph. Sound Reinforcement Handbook. 2nd ed. Hal Leonard Corporation. Milwaukee, Wisconsin. 1989. pp. 75 - 77
[3] Mikelson, Hans. "Interpolation", Csound Magazine, Summer 2000
[4] Boyd, Stephen. "Multitone Signals with Low Crest Factor". IEEE Transactions on Circuits and Systems, CAS-33(10):1018-1022, October 1986. Retrieved June 7, 2010 fromhttp://www.stanford.edu/~boyd/papers/multitone_low_crest.html
[5] Mercer, Colin. Posting of correspondence to alt.sci.physics.acoustics, March 27, 2000. Retrieved June 7, 2010 from http://www.cross-spectrum.com/audio/articles/center_frequencies.html
[6] Joaquin, Jacob. "Add_Synth, F-Table Based Additive Synthesizer", Csound Journal, Issue 13, Spring 2010
Additional Resources
Metzler, Bob. "Audio Measurement Handbook". Audio Precision, Inc. Beaverton, Oregon. 1993Anderson, Brad. "Crest factor analysis for complex signal processing".Retrieved June 7, 2010 from http://mobiledevdesign.com/hardware_news/radio_crest_factor_analysis/
Voxengo. "Span". Real-time fast Fourier transform audio spectrum analyzer plug-in. Retrieved June 7, 2010 from http://www.voxengo.com/product/span/
List of example .csd files (found in workbench_exs.zip):| chirp.csd |
| db.csd |
| frequency.csd |
| multch.csd |
| multitone.csd |
| nthroot.csd |
| noise_rand.csd |
| oscillator.csd |
| pinknoise.csd |
| pulsetrain.csd |
| sine.csd |
| sweep20_20khz_44_16.csd |
| sweep20_20khz_48_24.csd |
| sweep_dwell.csd |
| third_octave.csd |
| third_octave_play.csd |
| third_octave_base10.csd |
| waves.csd |
| whitenoise.csd |
| xclass.csd |