Csound Journal

Introduction

In the old time of analog synthesizers, producing complex sounds was easyby connecting the audio output of one VCO to the frequency control input of anotherVCO and connecting the audio output of the latter to the frequency control inputof the first one. This simple patch could yield a chaotic result as illustrated byDan Slater [1]. Our article describes a Csound plugin presenting a few opcodesimplementing such patches.

I. Overview

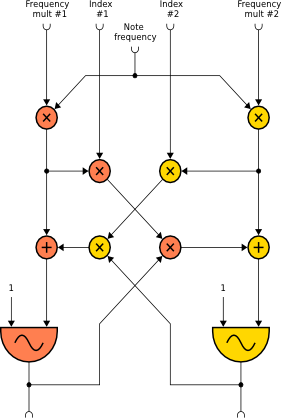
crossfm

The crossfm and crossfmi opcodes implement cross frequency modulationbetween two oscillators as shown in the following diagram:

Figure 1. Diagram of the crossfm opcode.

The syntax is:

a1, a2 crossfm xfrq1, xfrq2, xndx1, xndx2, kcps, ifn1, ifn2 [, iphs1] [, iphs2]a1, a2 crossfmi xfrq1, xfrq2, xndx1, xndx2, kcps, ifn1, ifn2 [, iphs1] [, iphs2]

where the parameters are:

xfrq1 -- a parameter that, when multiplied by the kcps parameter, gives the frequency of oscillator #1.
xfrq2 -- a parameter that, when multiplied by the kcps parameter, gives the frequency of oscillator #2.
xndx1 -- the index of the modulation of oscillator #2 by oscillator #1.
xndx2 -- the index of the modulation of oscillator #1 by oscillator #2.
kcps -- a common base value, in cycles per second, for both oscillator frequencies.
ifn1 -- function table number for oscillator #1 (usually a sinewave).
ifn2 -- function table number for oscillator #2 (usually a sinewave).
iphs1 (optional, default=0) -- initial phase of waveform in table ifn1, expressed as a fraction of a cycle (0 to 1). A negative value will cause phase initialization to be skipped.
iphs2 (optional, default=0) -- initial phase of waveform in table ifn2, expressed as a fraction of a cycle (0 to 1). A negative value will cause phase initialization to be skipped.

crossfmi behaves like crossfm except that linear interpolation is used for table lookup.

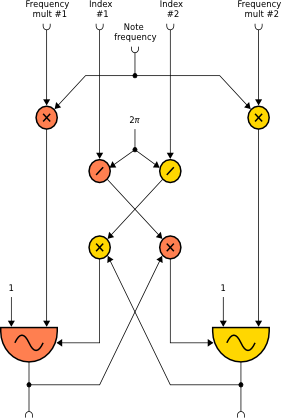
crosspm

The crosspm and crosspmi opcodes implement cross phase modulationbetween two oscillators as shown in the following diagram:

Figure 2. Diagram of the crosspm opcode.

The syntax is:

a1, a2 crosspm xfrq1, xfrq2, xndx1, xndx2, kcps, ifn1, ifn2 [, iphs1] [, iphs2]a1, a2 crosspmi xfrq1, xfrq2, xndx1, xndx2, kcps, ifn1, ifn2 [, iphs1] [, iphs2]

where the parameters have the same meaning as in crossfm, and again crosspmiuses linear interpolation for table lookup.

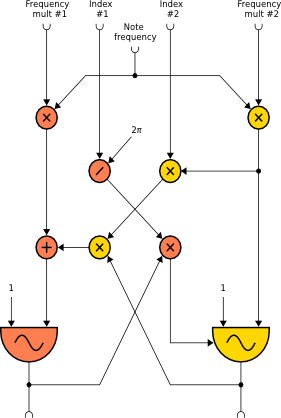
crossfmpm

Finally, the crossfmpm and crossfmpmi opcodes implement crossfrequency/phase modulation between two oscillators as shown in the followingdiagram:

Figure 3. Diagram of the crossfmpm opcode.

The syntax is:

a1, a2 crossfmpm xfrq1, xfrq2, xndx1, xndx2, kcps, ifn1, ifn2 [, iphs1] [, iphs2]a1, a2 crossfmpmi xfrq1, xfrq2, xndx1, xndx2, kcps, ifn1, ifn2 [, iphs1] [, iphs2]

where the parameters have the same meaning as in crossfm, and crossfmpmi and uselinear interpolation for table lookup. Oscillator #1 is frequency-modulated byoscillator #2 while oscillator #2 is phase-modulated by oscillator #1.

II. Technical issues

Frequency modulation vs phase modulation

In frequency modulation, the frequency of the carrier is modified by the modulatorwhile in phase modulation, it is the phase of the carrier that is modified. Insingle modulation, the audio result is the same with both modulations, even though thealgorithms are different. On the other hand, if we introduce feedback loops likein the opcodes above, the audio result from frequency modulation will differ fromthe phase modulation one. This is due to the fact that each oscillator beingmodulated, their waveforms become complex and a dc component may appear in theirspectra. This dc component may be considered as having a frequency of 0 Hz. Ifthe oscillator is frequency modulated, this 0 Hz component will be shifted bythe modulation like the other frequencies, thus becoming audible. Conversely, ifthe oscillator is phase modulated, the dc component will remain aninaudible dc component (a more detailed explanation is given in the article byRussel Pinkston in "The Csound Book" [2]).

In normal use, people often prefer phase modulation in order to avoid the annoyance ofthe dc shift, especially if the purpose is to mimic acoustic instruments as withthe famous DX7 synthesizers by Yamaha in the 1980's. Here, on the contrary, wewill take advantage of this feature in the cross frequency modulation.

Sampling rate

Usually, opcodes are supposed to operate in the same way, irrespective of thesampling rate value, with the only difference that a higher sampling rate yields abroader bandwidth and thus a better sound quality. In cross frequency modulation,we can have very rich spectra, especially with high modulation indexes, and insome cases foldover aliases may occur if the sampling rate is not highenough. Moreover with non-linear feedback loops a different sampling rate meansa different step size in the algorithm difference equations and then a differentaudio result due to the non-linearity of the algorithm. In Csound, two otheropcodes have the same characteristics: planet and chuap.

We can hear this in the following example: artefacts.ogg.Four notes are played by crossfm with the same parameters (frq1=517.505,frq2=735.696, ndx1=3, and ndx2=3) but increasing samplingrate (48kHz, 96kHz, 192kHz, and 384kHz).

When working with those opcodes, you should use a sampling rate as high aspossible. If you need to produce a CD quality file, you should first producea high sampling rate file and then downsample this file using thesrconv utility, with a command like this:

srconv -Q 4 -r 44100 -W -s -o cdqualityfile.wav highsrfile.wav

The plugin source code

The plugin source code is given in this archivefile. If you adapt the included Makefile to your environment, you can use it tobuild the plugin. More information about plugin opcodes is available at [4].

III. Exploring the parameter space

A GUI for testing

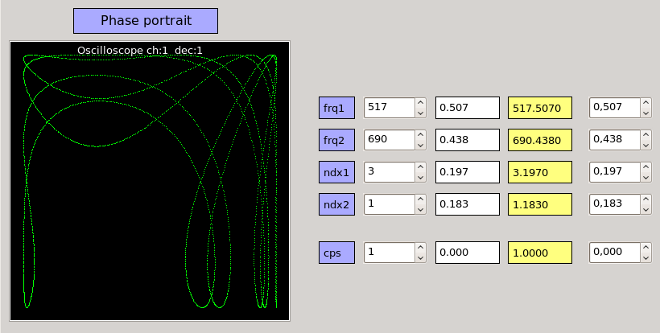
We can use Qutecsound ([3]) and its widget set to build a friendly GUI to explorethe different values of the parameters. The oscilloscope widget was modified so thatit can display Lissajou curves or Poincaré maps. This new feature is available inthe version 0.4.5 of Qutecsound.

The cfmgui.csd file can be used as a testing GUI forcrossfm. Each parameter can be set via a coarse value spin box for itsinteger part, a fine value scroll number and/or spin box for its decimal part. Thestereo output of the instrument is displayed through the oscilloscope widget asa phase portrait (Lissajou curve mode):

Figure 4. Widget panel of cfmgui.csd in Qutecsound.

Automated exploration

Besides using the GUI described above to test the parameters, we can use interactivegenetic algorithms as described by Colin G. Johnson [5]. Geneticsalgorithms are exploration tools based upon natural selection and genetics.

A population of individuals is randomly created. Each individual represents a set ofparameters to control the orchestra for the generation of one single note. The parametersare concatenated into a "chromosome" as a binary string. Each individual receives a fitnessvalue. Usually, this fitness value is calculated from an optimization function. Here, weuse instead a set of sliders in a graphical interface to manually set the fitness value ofeach sound (this is the interactive part). A new generation is then processed by selectingindividuals in the old generation in function of their fitness, recombination of theselected individuals (crossover) and mutation.

The "blue" frontend ([6]) with its scripting language Jython (a Javawritten version of Python) is a good candidate to implement a Simple Genetic Algorithm.The cfm_ga.blue file has a Score Timeline including foursoundObjects. The first one is a Comment describing the project. The second one is aPythonObject implementing the classes of a Simple Genetic Algorithm as described in([7]). The following diagram shows the classes:

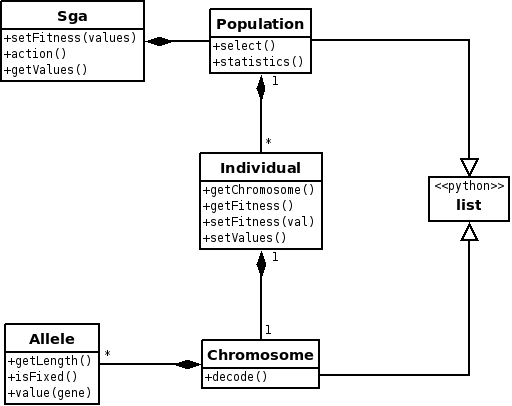
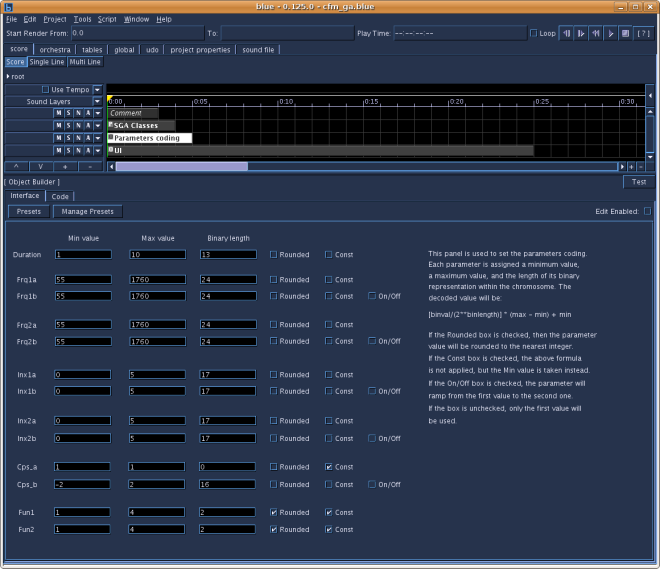
Figure 5. Classes of the Simple Genetic Algorithm.

The third soundObject is an ObjectBuilder that displays an interface for the parameterscoding. Each parameter is given min and max values and the number of bits of its binary coding within the binary string (chromosome). Some parameters have 'a' and'b' entries. This means that if the 'b' entry is activated, the parameter value willramp between the 'a' and 'b' values during the note length. The parametersare input arguments for one of the three orchestras; for example the crossfm testorchestra is:

idur      =         p3iamp      =         p4ifq1a     =         p5ifq1b     =         p6ifq2a     =         p7ifq2b     =         p8inx1a     =         p9inx1b     =         p10inx2a     =         p11inx2b     =         p12icpsa     =         p13icpsb     =         p14ifn1      =         p15ifn2      =         p16iphs1     =         p17iphs2     =         p18kfrq1     line      ifq1a, idur, ifq1bkfrq2     line      ifq2a, idur, ifq2bkndx1     line      inx1a, idur, inx1bkndx2     line      inx2a, idur, inx2bkcps      line      icpsa, idur, icpsbkenv      linen     iamp, 0.05, idur, 0.2a1, a2    crossfm   kfrq1, kfrq2, kndx1, kndx2, kcps, ifn1, ifn2, iphs1, iphs2          outs      a1*kenv, a2*kenv

Figure 6. Parameters coding interface.

The fourth soundObject is an ObjectBuilder that displays the user interface (UI) forrunning the genetic algorithm.

Figure 7. User Interface.

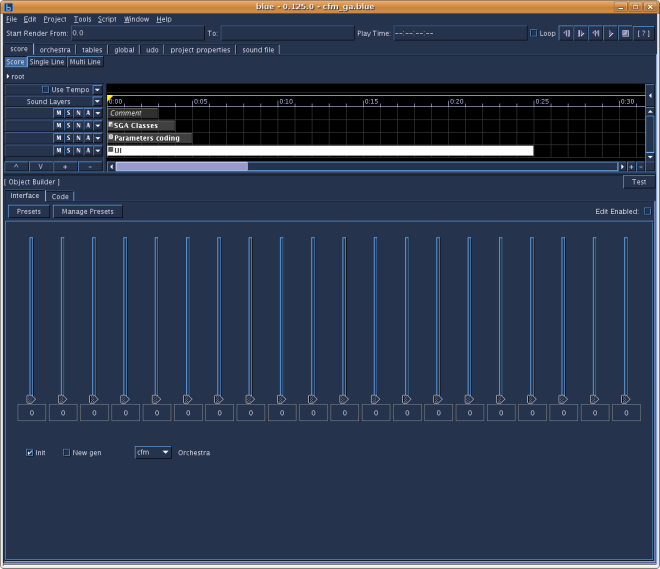
You first have to select the Parameters Coding soundObjectand choose the settings you want. Then you select the UI soundObject. Each time youpress the play button, one of three possibilities happens. If the Init box is checked,a new SGA is initiated with its first generation randomly calculated. If the Initbox is unchecked and the New gen box is unchecked, you hear again the sounds of the lastcalculated generation. This is useful to set correctly the fitness values (slider controls).Finally, if the Init box is unchecked and the New gen box is checked, a new generation iscalculated by the SGA depending on the fitness values set by the user.

Note: the first time you hit the play button, the Init box MUST be checked, otherwise you willget a Jython error. This is due to the fact that when you open the cfm_ga.blue file, the ga objectdoes not exist within the Jython memory space, and the only way to create a new ga object is tohit the play button while the UI Init box is checked.

IV. Examples

The first example (ex01.csd) is a continuous sound withfixed frequencies, while the modulation indexes are moving along a ramp. To get morerelief, the sound is granulated through instrument #2.(ex01.ogg)

The second example (ex02.csd) is a pseudo-melody withan exotic tuning that is obtained by varying the modulation indexes. The firstnote is played using two sine waves. The second note is played using two pseudo-square waveswith the modulation indexes variation reversed: the "melody" seems played backwards andthe timbre is richer. The third note is like the first one but it is two seconds longerand thus the "melody" is slower. The fourth note is like the second one, but with twosine waves, longer duration and the second frequency one Hz higher, giving a richer tremolo.(ex02.ogg)

The third example (ex03.csd) uses cross phase modulationto simulate an old airplane engine. The function table used is a pseudo-sawtooth waveform.Note that the Ogg Vorbis compression algorithm haschanged the original sound. You should play the example from csound to hear the originalsound. (ex03.ogg)

Conclusion

Csound is a powerful and ubiquitous software. In this article it has been shown howCsound can be used to build specific tools adapted for particular research. Thanks tothe developers, rich frontends exist for Csound that allow us to rapidly test new ideasand build exploration tools. In 1963, the composer Iannis Xenakis wrote in the firstFrench edition of his famous book "Musiques Formelles" ([8]):"With the aid of electronic computers the composer becomes a sort of pilot: he pressesthe buttons, introduces coordinates, and supervises the controls of a cosmic vesselsailing in the space of sound, across sonic constellations and galaxies that he couldformerly glimpse only as a distant dream. Now he can explore them at his ease, seatedin an armchair". In 1963 this type of writing could be considered visionary writing, buttoday it is a reality.

Acknowledgements

I want to thank Andrés Cabrera for giving me technical informations to modify theQuteCsound oscilloscope widget so that it could display Lissajou curves. Thanks toSteven Yi and to Victor Lazzarini for sending me references about frequencymodulation and feedback oscillators. Finally I would like to thank the editors JamesHearon and Steven Yi for giving me extra time to develop the genetic algorithms section.